Здравствуйте, Дорогие друзья! Карантин. Есть время порешать задачи.



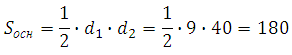


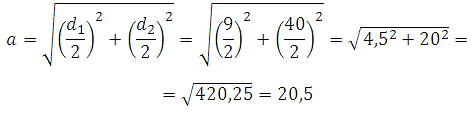


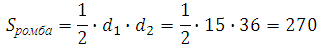


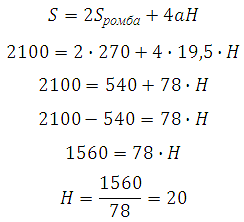
Ответ: 20
27062. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
Посмотреть решение
27148. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
В будущем вас ожидают задачи с пирамидами, не пропустите.
На этом всё. Успеха вам!
С уважением, автор проекта "Математика? Легко!!!"

Здесь представлены две задачи, связанные с площадью поверхности прямого параллелепипеда.
Это взаимообратные задачи: в одной даны диагонали ромба, лежащего в основании и боковое ребро, требуется найти площадь поверхности параллелепипеда; в другой задаче дана площадь поверхности, диагонали ромба, лежащего в основании и требуется найти боковое ребро.
Напомню формулы. Площадь поверхности прямой призмы:
Напомню формулы. Площадь поверхности прямой призмы:

Так же для нахождения площади ромба будет использована формула площади четырёхугольника:
Понятно, что диагонали ромба пересекаются под углом 900. Известно, что синус этого угла равен единице, поэтому формула примет вид:

Рассмотрим задачи:
ЗАДАЧА
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 9 и 40, и боковым ребром, равным 55.
Площадь поверхности данной призмы равна сумме площадей оснований и четырёх боковых граней:
Основание призмы – ромб, его площадь мы найдём по формуле:

Значит:
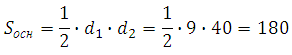
Так как призма прямая, то её высота равна боковому ребру:
Используя теорему Пифагора можем выразить сторону ромба через его диагонали d1 и d2 как:

Значит:
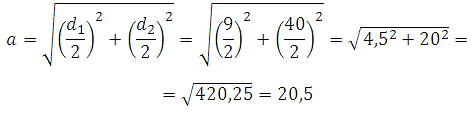
Тогда площадь поверхности призмы равна:
Ответ: 4870
ЗАДАЧА
В основании прямой призмы лежит ромб с диагоналями, равными 15 и 36. Площадь ее поверхности равна 2100. Найдите боковое ребро этой призмы.
Данная задача является обратной предыдущей. Здесь известна площадь поверхности и требуется найти боковое ребро. У прямой призмы боковое ребро равно её высоте.
Запишем формулу площади поверхности призмы:

Площадь поверхности известна, значит нам необходимо найти площадь ромба лежащего в основании и его сторону.
Площадь ромба:
Используя теорему Пифагора можем выразить сторону ромба через его диагонали d1 и d2 как:

Значит:

Таким образом:
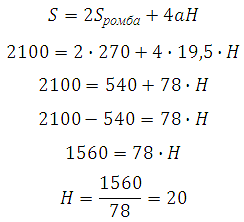
Ответ: 20
РЕШИТЕ САМОСТОЯТЕЛЬНО
27062. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
Посмотреть решение
27148. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
На этом всё. Успеха вам!
С уважением, автор проекта "Математика? Легко!!!"





Ребята, успеха вам в решении задачи.
ОтветитьУдалитьРешайте, решайте! Логику развивайте!
ОтветитьУдалитьВ этом году в наших школах в 9 классах ГИА будет проходить в режиме ЕГЭ. Очень хочется, чтобы ребята справились с заданиями.
ОтветитьУдалить