«Задачи на проценты. Часть 1. Задачи В1»
Здравствуйте, Дорогие Друзья! В этой статье мы рассмотрим некоторые задачи на проценты. Вообще, как показывает статистика, при сдаче ЕГЭ по математике, задачи В1 трудностей не вызывают, их решают 9 из 10 выпускников. Возникает вопрос: всё же, в каких задачах допускаются ошибки? Как правило это задачи на проценты, номера прототипов этих задач перечислены на странице «ЗАДАЧИ В1».
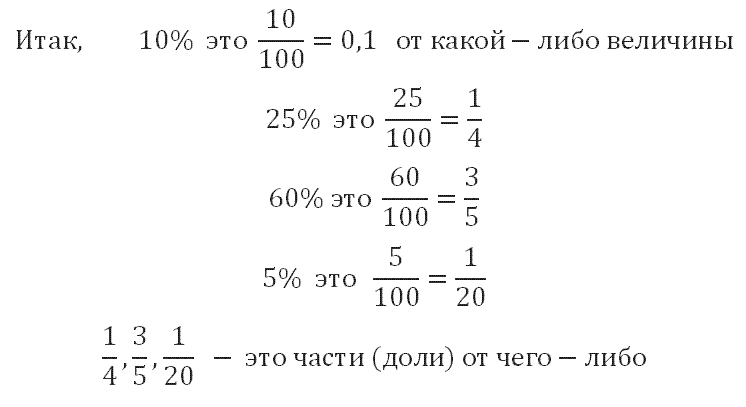 Например, если выразить в долевом отношении 25% от килограмма конфет, то это будет одна четверть от килограмма. Части (доли) могут быть представлены не только в виде обыкновенной дроби, но и в виде десятичной, например: 0,25; 0,6; 0,05; 0,56.
Например, если выразить в долевом отношении 25% от килограмма конфет, то это будет одна четверть от килограмма. Части (доли) могут быть представлены не только в виде обыкновенной дроби, но и в виде десятичной, например: 0,25; 0,6; 0,05; 0,56.
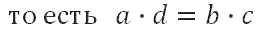 Если какая-либо величина в пропорции неизвестна, ее можно найти именно по этому правилу. например, из пропорции:
Если какая-либо величина в пропорции неизвестна, ее можно найти именно по этому правилу. например, из пропорции:
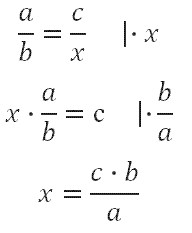 Для решения используйте тот способ, который вам удобен. Чтобы составить пропорцию при решении задач на проценты, необходимо установить некоторое соответствие между процентами и количеством чего-либо (рубли, детали, шубы, изделия и т.п.). По рассмотренным примерам вы это поймёте, что это значит.
Для решения используйте тот способ, который вам удобен. Чтобы составить пропорцию при решении задач на проценты, необходимо установить некоторое соответствие между процентами и количеством чего-либо (рубли, детали, шубы, изделия и т.п.). По рассмотренным примерам вы это поймёте, что это значит.
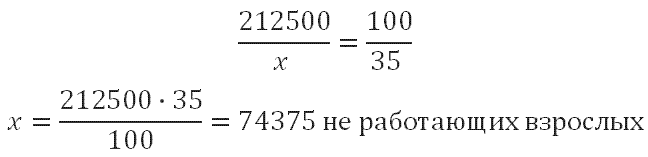 Значит, число работающих взрослых составляет 212500-74375=138125 человек. При решении данного типа задач будьте внимательны, есть соблазн записать промежуточный результат, например, 74375. Внимательно читайте условие, и не теряйте из виду, что необходимо найти.
Значит, число работающих взрослых составляет 212500-74375=138125 человек. При решении данного типа задач будьте внимательны, есть соблазн записать промежуточный результат, например, 74375. Внимательно читайте условие, и не теряйте из виду, что необходимо найти.
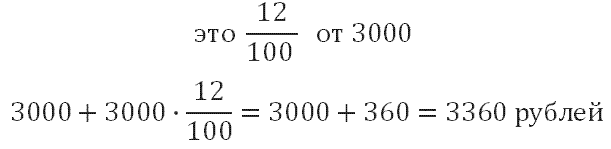 Вы можете сначала составить пропорцию, найти 12% от 3000, а затем сложить. Ещё раз повторюсь, решайте так, как вам удобнее и понятнее.
Вы можете сначала составить пропорцию, найти 12% от 3000, а затем сложить. Ещё раз повторюсь, решайте так, как вам удобнее и понятнее.
Здравствуйте, Дорогие Друзья! В этой статье мы рассмотрим некоторые задачи на проценты. Вообще, как показывает статистика, при сдаче ЕГЭ по математике, задачи В1 трудностей не вызывают, их решают 9 из 10 выпускников. Возникает вопрос: всё же, в каких задачах допускаются ошибки? Как правило это задачи на проценты, номера прототипов этих задач перечислены на странице «ЗАДАЧИ В1».
Урок 2
Там же есть ссылки на них.
Теперь немного теории. В большинстве задач В1 используется понятие — процент. Все в быту сталкиваются с этим понятием и используют его. Даже не изучая никакой теории, мы понимаем, что 50% это половина чего-то, 10% это десятая часть чего-то, 100% это полностью это «что-то». Вспомним, что
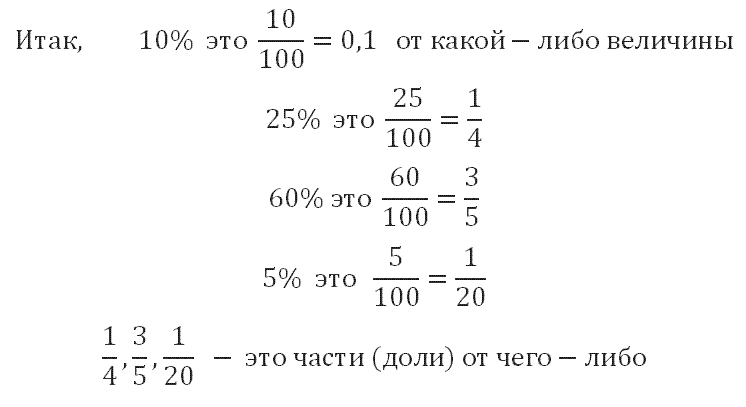 Например, если выразить в долевом отношении 25% от килограмма конфет, то это будет одна четверть от килограмма. Части (доли) могут быть представлены не только в виде обыкновенной дроби, но и в виде десятичной, например: 0,25; 0,6; 0,05; 0,56.
Например, если выразить в долевом отношении 25% от килограмма конфет, то это будет одна четверть от килограмма. Части (доли) могут быть представлены не только в виде обыкновенной дроби, но и в виде десятичной, например: 0,25; 0,6; 0,05; 0,56.
Что такое дробь (часть) от числа? Когда мы говорим: «одна четверть от х» — это значит, что
* * * * * * *
Чтобы найти дробь (или часть) от числа, надо дробь (часть) умножить на это число.
Задачи на проценты решаются путём составления пропорции. Напомним, что пропорция — это равенство вида:
Основное правило пропорции: произведение крайних членов равно произведению средних:
Для кого-то будет удобным следующее правло. Его ещё называют «правило креста». Чтобы обойтись без лиших записей и вы не задумывались в дальнейшем, как правильно посчитать и не ошибиться, запомните – где бы в пропорции не стоял х, его мы находим следующим образом: записываем х, ставим знак равенства, далее дробь, в числитель записываем произведение известных членов стоящих по диагонали, в знаменатель то значение, которое стоит по диагонали от х. Название этого правила исходит от пересечения диагоналей, они образуют крест:
Кроме того, можно обойтись без этого правила, и решать пропорцию как простое линейное уравнение (имеем право умножать или делить обе части уравнения на одно и то же число):
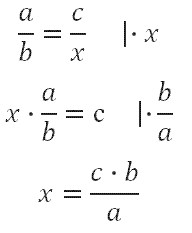 Для решения используйте тот способ, который вам удобен. Чтобы составить пропорцию при решении задач на проценты, необходимо установить некоторое соответствие между процентами и количеством чего-либо (рубли, детали, шубы, изделия и т.п.). По рассмотренным примерам вы это поймёте, что это значит.
Для решения используйте тот способ, который вам удобен. Чтобы составить пропорцию при решении задач на проценты, необходимо установить некоторое соответствие между процентами и количеством чего-либо (рубли, детали, шубы, изделия и т.п.). По рассмотренным примерам вы это поймёте, что это значит.ЗАПОМНИМ ВАЖНОЕ ПРАВИЛО:
за 100% принимается та величина, с которой мы сравниваем.
Обратите внимание, что 3025 рублей это цена, после повышения на 21%. При составлении пропорции мы запишем: 3025 это 121%, а стоимость до повышения примем за 100% (помните правило – за 100% процентов принимаем величину, с которой сравниваем).
3025 рубля - 121%
х рублей - 100%
То есть решим обратную задачу: чайник стоит 2500 рублей, цена повысилась на 21%. Какова его стоимость после повышения?
Составляем пропорцию, 2500 рублей принимаем за 100%, х рублей принимаем за 121% (цена, повышенная на 21%):
2500 рублей - 100%
х рублей - 121%
Ответ: 2500
Определим, сколько процентов от 1200 рублей составляет сниженная цена. 1200 рублей (величина, с которой сравниваем) принимаем за 100%, 972 рубля это х %. Составляем пропорцию:
1200 рублей - 100%
972 рубля - х %
То есть 972 это 81% от 1200 рублей.
Значит, цена снизилась на 100-81=29%.
Ответ: 29
Почему-то именно эту задачу редко решают правильно? Дело в том, что «15 процентов» или «35 процентов» — величины относительные. Каждый раз за сто процентов могут приниматься разные величины. Помните правило: за сто процентов принимается в каждом случае то, с чем мы сравниваем. Итак, дети и подростки составляют 15% от 250000 жителей. Значит, их число — это 15% от 250000,
Получили, что в городе 37500 детей и подростков. Следовательно, взрослых в городе 250000-37500=212500 человек.
Среди взрослых 35% не работает. Теперь за 100% мы принимаем число взрослых. Получается, что число не работающих взрослых жителей равно 35% от 212500, составляем пропорцию:
212500 - 100%
х - 35%
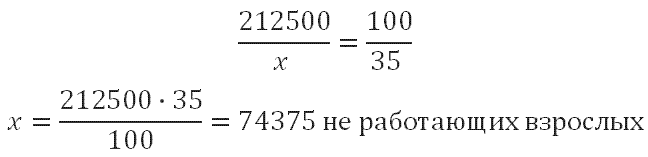 Значит, число работающих взрослых составляет 212500-74375=138125 человек. При решении данного типа задач будьте внимательны, есть соблазн записать промежуточный результат, например, 74375. Внимательно читайте условие, и не теряйте из виду, что необходимо найти.
Значит, число работающих взрослых составляет 212500-74375=138125 человек. При решении данного типа задач будьте внимательны, есть соблазн записать промежуточный результат, например, 74375. Внимательно читайте условие, и не теряйте из виду, что необходимо найти.
Ответ: 138125
Определим, сколько всего должен выплатить клиент, к сумме 3000 прибавим 12% от 3000 рублей:
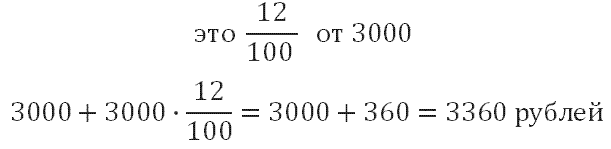 Вы можете сначала составить пропорцию, найти 12% от 3000, а затем сложить. Ещё раз повторюсь, решайте так, как вам удобнее и понятнее.
Вы можете сначала составить пропорцию, найти 12% от 3000, а затем сложить. Ещё раз повторюсь, решайте так, как вам удобнее и понятнее.
Теперь определим, сколько клиент будет выплачивать в месяц:
Составляем пропорцию и находим 13% от 10000 рублей:
10000 рублей - 100%
х рублей - 13 %
Иван Кузьмич получит после вычета: 10000-1300=8700 рублей.
Ответ: 8700
В разделе «Задачи В1» есть ещё задачи на проценты (без округления): 77340, 77341, 77342, 77343, 77344, 77345, 77346, 77347, 77348, 77349, 77353. 77354, 77356, 77365, а так же подобные тем, что мы рассмотрели выше. Скачайте прототипы задач В1, и посмотрите интересующие вас.
Не подписались на рассылку? Подписывайтесь. Получите 458 задач В6 с ответами, затем в течение 3 дней всю теорию для подготовки к ЕГЭ по математике от В1 до В14 (14 файлов PDF).
С уважением автор проекта «Математика? Легко!!!» Александр Крутицких.



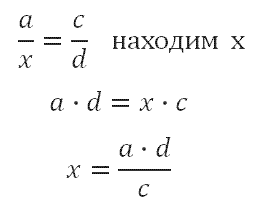
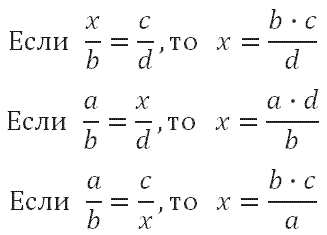

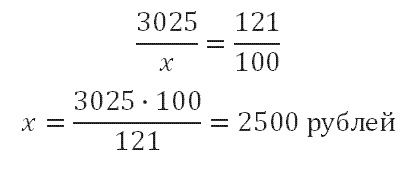
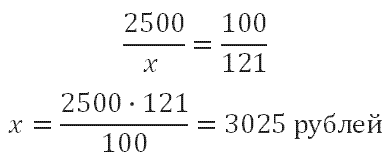

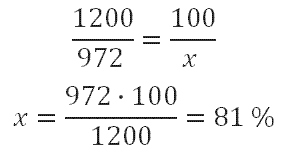

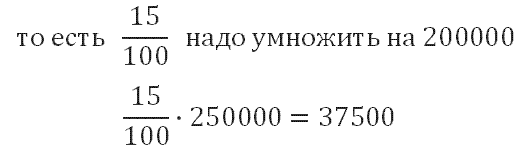


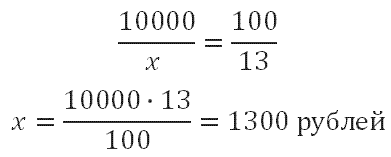
Комментариев нет:
Отправить комментарий